Equações biquadradas é uma equação escrita da seguinte forma geral: ax4 + bx2 + c = 0. Para resolver (encontrarmos as sua raízes) é preciso transformá-las em uma equação do segundo grau.
Para melhor compreensão veja no exemplo abaixo como essa transformação acontece e como chegamos às raízes da equação biquadrada.
y4 – 10y2 + 9 = 0 → equação biquadrada
(y2)2 – 10y2 + 9 = 0 → também pode ser escrita assim.
Substituindo variáveis: y2 = x, isso significa que onde for y2 iremos colocar x.
x2 – 10x + 9 = 0 → agora resolvemos essa equação do 2º grau encontrando x` e x``
a = 1 b = -10 c = 9
∆ = b2 – 4ac
∆ = (-10)2 – 4 . 1 . 9
∆ = 100 – 36
∆ = 64
x = - b ± √∆ 2a
x = -(-10) ± √64
2 . 1
x = 10 ± 8
2
x’ = 9
x” = 1
Essas são as raízes da equação x2 – 10x + 9 = 0, para encontrarmos as raízes da equação biquadrada y4– 10y2 + 9 = 0 devemos substituir os valores de x’ e x” em y2 = x.
Para x = 9
y2 = x
y2 = 9
y = √9
y = ± 3
Para x = 1
y2 = x
y2 = 1
y = √1
y = ±1
Portanto, a solução da equação biquadrada será:
S = {-3, -1, 1, 3}.
segunda-feira, 22 de julho de 2013
Relações entre Coeficientes e Raízes
Raízes de uma Equação do 2° grau
Abaixo temos as raízes de uma equação do segundo grau genérica:
Como já visto em outra página deste site, só existirão raízes reais para a equação, desde que Δ ≥ 0, pois não existe raiz quadrada real de um número negativo.
Soma das Raízes de Equações do 2° grau
Sendo x1 e x2 raízes de uma equação como definido acima, temos que a soma destas raízes será:
Logo a soma das raízes será dada por:
Produto das Raízes de Equações do 2° grau
Assim como no caso da soma, o produto das raízes x1 e x2 será:
Sabemos que Δ = b2 -4ac. Substituindo-o na equação temos:
Portanto o produto das raízes será dado por:
Construção de Equações do 2° grau a partir de suas Raízes
Através da fórmula geral de resolução, também conhecida como fórmula de Bhaskara, partimos de uma equação e chegamos às suas raízes. Agora, com base nas relações de Girard, veremos como a partir das raízes, chegarmos à equação.
A forma reduzida deste tipo de equação é ax2 + bx + c = 0. Realizando a divisão de ambos os membros por atemos:
Como supracitado nesta página:
E:
Chamemos de S a soma das raízes ( S = x1 + x2 ) e de P o seu produto ( P = x1 . x2 ). Substituindo na equação temos:
Portanto a equação x2 - Sx + P = 0, onde os coeficientes S e P representam respectivamente a soma e o produtodas raízes, nos permite reconstruir a equação que possui estas raízes.
Exemplo
Para a fixação dos conceitos, tomemos uma equação, identifiquemos as suas raízes e a partir delas, através das relações de Girard cheguemos à equação novamente.
Parta da equação do segundo grau x2 - 5x - 24 = 0, encontre as suas raízes e a partir delas reconstrua a equação original.
Em primeiro lugar vamos encontrar as raízes da equação x1 e x2:
Note que pudemos encontrar duas raízes reais e diferentes para equação, justamente porque Δ > 0. Veja que nesta equação o valor de Δ é 121.
Agora que já conhecemos as suas raízes, através das relações de Girard iremos reconstruir a equação original.
Para a soma das raízes temos:
Para o produto das raízes temos:
Reconstruindo temos:
Portanto partimos da equação x2 - 5x - 24 = 0, encontramos as suas raízes reais x1 = 8 e x2 = -3 e a partir da soma e do produto delas, reconstruímos a equação original.Equações Literais
As equações literais do 2º grau são conhecidas por possuírem os coeficientes representados por letras. Esse modelo de equação é utilizado no intuito de aprimorar o desenvolvimento da expressão de Bhaskara, dado os coeficientes numéricos das equações de 2º grau. Dessa forma, ao iniciar esse conteúdo, trabalhe a resolução desse modelo de equação, lembrando que uma equação literal possui como solução uma relação de dependência entre a incógnita e o coeficiente literal.
Apresente exemplos de equações literais do 2º grau e os coeficientes relacionados à incógnita da equação. Veja:
x² – 7ax + 10a² = 0 (a > 0)
Coeficientes:
a = 1
b = –7a
c = 10a²
Coeficientes:
a = 1
b = –7a
c = 10a²
x² – (m + 3)x + 3m = 0 (m > 3)
Coeficientes:
a = 1
b = m + 3
c = 3m
Coeficientes:
a = 1
b = m + 3
c = 3m
x² + 8mx = 0
Coeficientes:
a = 1
b = 8m
c = 0
Coeficientes:
a = 1
b = 8m
c = 0
px² – 4x + 4px = 0 (p ≠ 0)
Coeficientes:
a = p
b = –4x
c = 4p
Coeficientes:
a = p
b = –4x
c = 4p
Apresente modelos de equações literais resolvidas utilizando o método de Bhaskara para as equações completas e os métodos da fatoração para as incompletas.
Incompleta
x² + 8mx = 0 (aplicar fator comum em evidência)
x * (x + 8m) = 0
x * (x + 8m) = 0
x’ = 0
x + 8m = 0
x’’ = –8m
x’’ = –8m
Conjunto Solução: {x’ = 0 e x’’ = –8m}
Completa
x² – 3ax + 2a² = 0 (a > 0)
a = 1, b = –3a e c = 2a²
∆ = b² – 4ac
∆ = (–3a)² – 4 * 1 * 2a²
∆ = 9a² – 8a²
∆ = a²
∆ = (–3a)² – 4 * 1 * 2a²
∆ = 9a² – 8a²
∆ = a²
.jpg)
Conjunto Solução: {x’ = 2a e x’’ = a}
Resolução de equações completas do 2° grau (2°parte)
RESOLUÇÃO DE EQUAÇÃO INCOMPLETAS
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2° grau
1° CASO – equações da forma ax² + c = 0, (b = 0)
Exemplos:
1) x² - 25 = 0
x² = 25
x = √25
x = 5
logo V= (+5 e -5)
2) 2x² - 18 = 0
2x² = 18
x² = 18/2
x² = 9
x = √9
x = 3
logo V= (-3 e +3)
3) 7x² - 14 = 0
7x² = 14
x² = 14/7
x² = 2
x = √2
logo V = (-√2 e +√2)
4) x²+ 25 = 0
x² = -25
x = √-25
obs: não existe nenhum número real que elevado ao quadrado seja igual a -25
2° CASO: Equações da forma ax² + bx = 0 ( c = 0)
Propriedade: Para que um produto seja nulo é preciso que um dos fatores seja zero .
Exemplos
1) resolver x² - 5x = 0
fatorando x ( x – 5) = 0
deixando um dos fatores nulo temos x = 0
e o outro x – 5 = 0 , passando o 5 para o outro lado do igual temos x = 5
logo V= (0 e 5)
2) resolver: 3x² - 10x = 0
fatorando: x (3x – 10) = 0
deixando um dos fatores nulo temos x = 0
Tendo também 3x – 10 = 0
3x = 10
x = 10/3
logo V= (0 e 10/3)
Observe que, nesse caso, uma das raízes é sempre zero.
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2° grau
1° CASO – equações da forma ax² + c = 0, (b = 0)
Exemplos:
1) x² - 25 = 0
x² = 25
x = √25
x = 5
logo V= (+5 e -5)
2) 2x² - 18 = 0
2x² = 18
x² = 18/2
x² = 9
x = √9
x = 3
logo V= (-3 e +3)
3) 7x² - 14 = 0
7x² = 14
x² = 14/7
x² = 2
x = √2
logo V = (-√2 e +√2)
4) x²+ 25 = 0
x² = -25
x = √-25
obs: não existe nenhum número real que elevado ao quadrado seja igual a -25
2° CASO: Equações da forma ax² + bx = 0 ( c = 0)
Propriedade: Para que um produto seja nulo é preciso que um dos fatores seja zero .
Exemplos
1) resolver x² - 5x = 0
fatorando x ( x – 5) = 0
deixando um dos fatores nulo temos x = 0
e o outro x – 5 = 0 , passando o 5 para o outro lado do igual temos x = 5
logo V= (0 e 5)
2) resolver: 3x² - 10x = 0
fatorando: x (3x – 10) = 0
deixando um dos fatores nulo temos x = 0
Tendo também 3x – 10 = 0
3x = 10
x = 10/3
logo V= (0 e 10/3)
Observe que, nesse caso, uma das raízes é sempre zero.
Resolução de equações completas do 2° grau (1°parte)
A fórmula quadrática de Sridhara (Bhaskara)
DEFINIÇÃO
Uma equação do 2º grau com uma variável tem a forma:
ax² + bx + c = 0
onde os números reais a, b e c são os coeficientes da equação, sendo que a deve ser diferente de zero. Essa equação é também chamada de equação quadrática, pois o termo de maior grau está elevado ao quadrado
x é a incógnita
a,b, e c números reais, chamados de coeficientes
Equação Completa do segundo grau
Uma equação do segundo grau é completa, se todos os coeficientes a, b e c são diferentes de zero.
Exemplos:
1) 2 x² + 7x + 5 = 0, onde a = 2, b = 7 e c = 5
2) 3 x² + x + 2 = 0, onde a = 3 , b = 1 e c = 2
3) x² -7 x + 10 = 0, onde a = 1, b = -7 e c = 10
4) 5x² - x -3 = 0, onde a = 5, b = -1 e c = -3
Resolução de equações completas do 2° grau
1) Δ > 0 , a equação te duas raízes reais e diferentes.
2) Δ = 0, a equação tem uma raiz
3) Δ < 0 , a equação não tem raízes reais
Mostraremos agora como usar a fórmula de Bhaskara para resolver a equação:
x² - 5 x + 6 = 0
1) Identificar os coeficientes: a = 1, b = -5, c = 6
2) Escrever o discriminante Δ = b²-4ac.
3) Calcular Δ = (-5)² -4×1×6 = 25-24 = 1
4) Escrever a fórmula de Bhaskara:
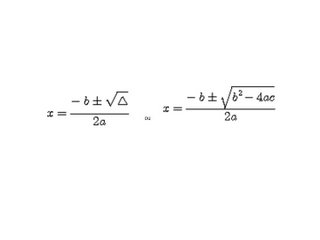
EXEMPLOS
Mostraremos na sequência como o matemático Sridhara, obteve a Fórmula (conhecida como sendo) de Bhaskara, que é a fórmula geral para a resolução de equações do segundo grau. Um fato curioso é que a Fórmula de Bhaskara não foi descoberta por ele mas pelo matemático hindu Sridhara, pelo menos um século antes da publicação de Bhaskara, fato reconhecido pelo próprio Bhaskara, embora o material construído pelo pioneiro não tenha chegado até nós.
O fundamento usado para obter esta fórmula foi buscar uma forma de reduzir a equação do segundo grau a uma do primeiro grau, através da extração de raízes quadradas de ambos os membros da mesma.
DEFINIÇÃO
Uma equação do 2º grau com uma variável tem a forma:
ax² + bx + c = 0
onde os números reais a, b e c são os coeficientes da equação, sendo que a deve ser diferente de zero. Essa equação é também chamada de equação quadrática, pois o termo de maior grau está elevado ao quadrado
x é a incógnita
a,b, e c números reais, chamados de coeficientes
Equação Completa do segundo grau
Uma equação do segundo grau é completa, se todos os coeficientes a, b e c são diferentes de zero.
Exemplos:
1) 2 x² + 7x + 5 = 0, onde a = 2, b = 7 e c = 5
2) 3 x² + x + 2 = 0, onde a = 3 , b = 1 e c = 2
3) x² -7 x + 10 = 0, onde a = 1, b = -7 e c = 10
4) 5x² - x -3 = 0, onde a = 5, b = -1 e c = -3
Resolução de equações completas do 2° grau
Como vimos, uma equação do tipo: ax² + bx + c= 0, é uma equação completa do segundo grau e para resolvê-la basta usar a fórmula quadrática (atribuída a Bhaskara), que pode ser escrita na forma:
Δ = b²- 4ac é o discriminante da equação.
Para esse discriminante Δ, há três possíveis situações:
1) Δ > 0 , a equação te duas raízes reais e diferentes.
2) Δ = 0, a equação tem uma raiz
3) Δ < 0 , a equação não tem raízes reais
Mostraremos agora como usar a fórmula de Bhaskara para resolver a equação:
x² - 5 x + 6 = 0
1) Identificar os coeficientes: a = 1, b = -5, c = 6
2) Escrever o discriminante Δ = b²-4ac.
3) Calcular Δ = (-5)² -4×1×6 = 25-24 = 1
4) Escrever a fórmula de Bhaskara:
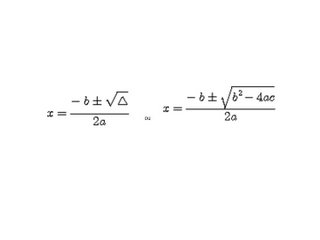
EXEMPLOS
Equação do 2º Grau
ma equação é uma expressão matemática que possui em sua composição incógnitas, coeficientes, expoentes e um sinal de igualdade. As equações são caracterizadas de acordo com o maior expoente de uma das incógnitas. Veja:
2x + 1 = 0, o expoente da incógnita x é igual a 1. Dessa forma, essa equação é classificada como do 1º grau.
2x² + 2x + 6 = 0, temos duas incógnitas x nessa equação, em que uma delas possui o maior expoente, determinado por 2. Essa equação é classificada como do 2º grau.
x³ – x² + 2x – 4 = 0, nesse caso temos três incógnitas x, em que o maior expoente igual a 3 determina que a equação é classificada como do 3º grau.
Cada modelo de equação possui uma forma de resolução. Trabalharemos a forma de resolução de uma equação do 2º grau, utilizando o método de Bhaskara. Determinar a solução de uma equação é o mesmo que descobrir suas raízes, isto é, o valor ou os valores que satisfazem a equação. Por exemplo, as raízes da equação do 2º grau x² – 10x + 24 = 0 são x = 4 ou x = 6, pois:
Substituindo x = 4 na equação, temos:
x² – 10x + 24 = 0
4² – 10 * 4 + 24 = 0
16 – 40 + 24 = 0
–24 + 24 = 0
0 = 0 (verdadeiro)
Substituindo x = 6 na equação, temos:
x² – 10x + 24 = 0
6² – 10 * 6 + 24 = 0
36 – 60 + 24 = 0
– 24 + 24 = 0
0 = 0 (verdadeiro)
Podemos verificar que os dois valores satisfazem a equação. Mas como determinarmos os valores que tornam a equação uma sentença verdadeira? É sobre essa forma de determinar os valores desconhecidos que abordaremos a seguir.
Vamos determinar pelo método resolutivo de Bhaskara os valores da seguinte equação do 2º grau: x² – 2x – 3 = 0.
Uma equação do 2º grau possui a seguinte lei de formação ax² + bx + c = 0, onde a, b e c são os coeficientes da equação. Portanto, os coeficientes da equação x² – 2x – 3 = 0 são a = 1, b = –2 e c = –3.
Na fórmula de Bhaskara utilizaremos somente os coeficientes. Veja:
.jpg)
1º passo: determinar o valor do discriminante ou delta (?)
? = b² – 4 * a * c
? = (–2)² – 4 * 1 * (–3)
? = 4 + 12
? = 16
2º passo
.jpg)
Os resultados são x’ = 3 e x” = –1.
Exemplo 2
Determinar a solução da seguinte equação do 2º grau: x² + 8x + 16 = 0.
Os coeficientes são:
a = 1
b = 8
c = 16
? = b² – 4 * a * c
? = 8² – 4 * 1 * 16
? = 64 – 64
? = 0
2x + 1 = 0, o expoente da incógnita x é igual a 1. Dessa forma, essa equação é classificada como do 1º grau.
2x² + 2x + 6 = 0, temos duas incógnitas x nessa equação, em que uma delas possui o maior expoente, determinado por 2. Essa equação é classificada como do 2º grau.
x³ – x² + 2x – 4 = 0, nesse caso temos três incógnitas x, em que o maior expoente igual a 3 determina que a equação é classificada como do 3º grau.
Cada modelo de equação possui uma forma de resolução. Trabalharemos a forma de resolução de uma equação do 2º grau, utilizando o método de Bhaskara. Determinar a solução de uma equação é o mesmo que descobrir suas raízes, isto é, o valor ou os valores que satisfazem a equação. Por exemplo, as raízes da equação do 2º grau x² – 10x + 24 = 0 são x = 4 ou x = 6, pois:
Substituindo x = 4 na equação, temos:
x² – 10x + 24 = 0
4² – 10 * 4 + 24 = 0
16 – 40 + 24 = 0
–24 + 24 = 0
0 = 0 (verdadeiro)
Substituindo x = 6 na equação, temos:
x² – 10x + 24 = 0
6² – 10 * 6 + 24 = 0
36 – 60 + 24 = 0
– 24 + 24 = 0
0 = 0 (verdadeiro)
Podemos verificar que os dois valores satisfazem a equação. Mas como determinarmos os valores que tornam a equação uma sentença verdadeira? É sobre essa forma de determinar os valores desconhecidos que abordaremos a seguir.
Vamos determinar pelo método resolutivo de Bhaskara os valores da seguinte equação do 2º grau: x² – 2x – 3 = 0.
Uma equação do 2º grau possui a seguinte lei de formação ax² + bx + c = 0, onde a, b e c são os coeficientes da equação. Portanto, os coeficientes da equação x² – 2x – 3 = 0 são a = 1, b = –2 e c = –3.
Na fórmula de Bhaskara utilizaremos somente os coeficientes. Veja:
1º passo: determinar o valor do discriminante ou delta (?)
? = b² – 4 * a * c
? = (–2)² – 4 * 1 * (–3)
? = 4 + 12
? = 16
2º passo
Os resultados são x’ = 3 e x” = –1.
Exemplo 2
Determinar a solução da seguinte equação do 2º grau: x² + 8x + 16 = 0.
Os coeficientes são:
a = 1
b = 8
c = 16
? = b² – 4 * a * c
? = 8² – 4 * 1 * 16
? = 64 – 64
? = 0
.jpg)
No exemplo 2 devemos observar que o valor do discriminante é igual a zero. Nesses casos, a equação possuirá somente uma solução ou raiz única.
Exemplo 3
Calcule o conjunto solução da equação 10x² + 6x + 10 = 0, considerada de 2º grau.
? = b² – 4 * a * c
? = 6² – 4 * 10 * 10
? = 36 – 400
? = –364
Nas resoluções em que o valor do discriminante é igual ou menor que zero, isto é, o número seja negativo, a equação não possui raízes reais.
sexta-feira, 26 de abril de 2013
Multiplicação e divisão de radicais
MULTIPLICAÇÃO E DIVISÃO:
√a * √b = √(a*b)
√4*√9 = √(4*9) = √36 = 6
para radicais de um mesmo índice, é só multiplicar seus radicandos.Para a divisão, é só dividir:
√a / √b = √(a/b)
√8 / √2 = √(8/2) = √4 = 2
Para radicais de índices diferentes:
É só tirar o MMC dos índices:
ex:
³√7 * √8 =
MMC (3,2) = 6
raiz sexta(7² * 8³)
Pra dividir é a mesma coisa:
√3 / ³√5² = raiz sexta(3³ / 5^4)
divide o índice do mmc pelo índice da raiz e joga no índice do radicando(cuidado se tiver um expoente no radicando)
ver regras de potenciação!
(5³)² = 5^6
(3¹²)³ = 3^15
√a * √b = √(a*b)
√4*√9 = √(4*9) = √36 = 6
para radicais de um mesmo índice, é só multiplicar seus radicandos.Para a divisão, é só dividir:
√a / √b = √(a/b)
√8 / √2 = √(8/2) = √4 = 2
Para radicais de índices diferentes:
É só tirar o MMC dos índices:
ex:
³√7 * √8 =
MMC (3,2) = 6
raiz sexta(7² * 8³)
Pra dividir é a mesma coisa:
√3 / ³√5² = raiz sexta(3³ / 5^4)
divide o índice do mmc pelo índice da raiz e joga no índice do radicando(cuidado se tiver um expoente no radicando)
ver regras de potenciação!
(5³)² = 5^6
(3¹²)³ = 3^15
Assinar:
Postagens (Atom)